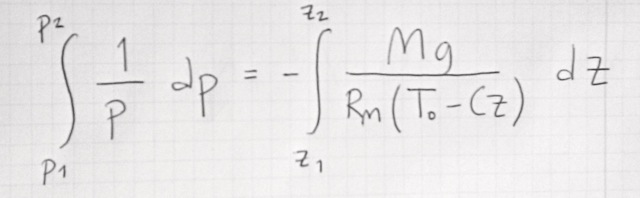Något av det häftigaste med att läsa till ingenjör är alla de verktyg du får längs vägen som fullständigt och oåterkalleligt förändrar hur du ser på världen. En bro är inte längre bara något du åker över med bilen, ett kylskåp inte ett mysterium och en zeppelinare inte bara något som flyger över huvudet på dig med hjälp av någon magisk kraft.
Något av det häftigaste med att läsa till ingenjör är alla de verktyg du får längs vägen som fullständigt och oåterkalleligt förändrar hur du ser på världen. En bro är inte längre bara något du åker över med bilen, ett kylskåp inte ett mysterium och en zeppelinare inte bara något som flyger över huvudet på dig med hjälp av någon magisk kraft.
I förra veckan i Termodynamiken fick vi en inlämningsuppgift som gick ut på att fundera på och räkna kring hur en zeppelinare fungerar. Hur ser kraften ut som får den att “lyfta” och hur högt kan den flyga? Det är sånt här jag älskar med KTH, att titta på ett verkligt fenomen och sedan skaffa sig en helt ny förståelse för vad som verkligen händer.
Hur som, första delen av uppgiften bestod i att bestämma hur lyftkraften varierar med höjden. Det man kallar lyftkraft i det här fallet bygger på Archimedes princip, nämligen att “ett föremål nedsänkt i vätska påverkas av en uppåtriktad kraft, som är lika stor som tyngden av den undanträngda vätskan”. Detta kan appliceras även på zeppelinare i mediet luft med vissa förändringar. Såhär ser formeln för lyftkraften ut:
För att kunna lösa uppgiften var vi tvungna att härleda fram ett uttryck för hur trycket förändras med höjden (se nedan) och sedan använda det framräknade trycket för att ta fram luftens densitet för varje given höjd. Mycket matte för att vara Termo och apropå det, ni som kämpar med Envariabeln eller Flervariabeln just nu: ge inte upp! Ni kommer att behöva allt det ni lär er nu i kurserna som kommer sen!
Slutuppgiften bestod sedan i att räkna ut zeppelinarens maxhöjd, d.v.s när formeln för lyftkraften är lika med noll eller när zeppelinarens tyngd är lika med den faktiska lyftkraften. Svaret blev kring 9000 meter för min zeppelinare.
Inte illa för en förvuxen heliumballong, eller vad säger ni?
Formelförklaring: